The JASP guidelines for conducting and reporting a Bayesian analysis

Despite the increasing popularity of Bayesian inference in empirical research, few practical guidelines provide detailed recommendations for how to apply Bayesian procedures and interpret the results. Here we offer specific guidelines for four different stages of Bayesian statistical reasoning in a research setting: planning the analysis, executing the analysis, interpreting the results, and reporting the results. The guidelines for each stage are illustrated with a running example. Although the guidelines are geared towards analyses performed with the open-source statistical software JASP, most guidelines extend to Bayesian inference in general.

Similar content being viewed by others

Bayesian Analysis Reporting Guidelines

Four reasons to prefer Bayesian analyses over significance testing

How to become a Bayesian in eight easy steps: An annotated reading list

Avoid common mistakes on your manuscript.

In recent years, Bayesian inference has become increasingly popular, both in statistical science and in applied fields such as psychology, biology, and econometrics (e.g., Andrews & Baguley, 2013; Vandekerckhove, Rouder, & Kruschke, 2018). For the pragmatic researcher, the adoption of the Bayesian framework brings several advantages over the standard framework of frequentist null-hypothesis significance testing (NHST), including (1) the ability to obtain evidence in favor of the null hypothesis and discriminate between “absence of evidence” and “evidence of absence” (Dienes, 2014; Keysers, Gazzola, & Wagenmakers, 2020); (2) the ability to take into account prior knowledge to construct a more informative test (Gronau, Ly, & Wagenmakers, 2020; Lee & Vanpaemel, 2018); and (3) the ability to monitor the evidence as the data accumulate (Rouder, 2014). However, the relative novelty of conducting Bayesian analyses in applied fields means that there are no detailed reporting standards, and this in turn may frustrate the broader adoption and proper interpretation of the Bayesian framework.

Several recent statistical guidelines include information on Bayesian inference, but these guidelines are either minimalist (Appelbaum et al., 2018; The BaSiS group, 2001), focus only on relatively complex statistical tests (Depaoli & Schoot, 2017), are too specific to a certain field (Spiegelhalter, Myles, Jones, & Abrams, 2000; Sung et al., 2005), or do not cover the full inferential process (Jarosz & Wiley, 2014). The current article aims to provide a general overview of the different stages of the Bayesian reasoning process in a research setting. Specifically, we focus on guidelines for analyses conducted in JASP (JASP Team, 2019; jasp-stats.org), although these guidelines can be generalized to other software packages for Bayesian inference. JASP is an open-source statistical software program with a graphical user interface that features both Bayesian and frequentist versions of common tools such as the t test, the ANOVA, and regression analysis (e.g., Marsman & Wagenmakers, 2017; Wagenmakers et al., 2018).

We discuss four stages of analysis: planning, executing, interpreting, and reporting. These stages and their individual components are summarized in Table 1. In order to provide a concrete illustration of the guidelines for each of the four stages, each section features a data set reported by Frisby and Clatworthy (1975). This data set concerns the time it took two groups of participants to see a figure hidden in a stereogram—one group received advance visual information about the scene (i.e., the VV condition), whereas the other group did not (i.e., the NV condition). Footnote 1 Three additional examples (mixed ANOVA, correlation analysis, and a t test with an informed prior) are provided in an online appendix at https://osf.io/nw49j/. Throughout the paper, we present three boxes that provide additional technical discussion. These boxes, while not strictly necessary, may prove useful to readers interested in greater detail.

Once the quality of the data has been confirmed, the planned analyses can be carried out. JASP offers a graphical user interface for both frequentist and Bayesian analyses. JASP 0.10.2 features the following Bayesian analyses: the binomial test, the Chi-square test, the multinomial test, the t test (one-sample, paired sample, two-sample, Wilcoxon rank-sum, and Wilcoxon signed-rank tests), A/B tests, ANOVA, ANCOVA, repeated measures ANOVA, correlations (Pearson’s ρ and Kendall’s τ), linear regression, and log-linear regression. After loading the data into JASP, the desired analysis can be conducted by dragging and dropping variables into the appropriate boxes; tick marks can be used to select the desired output.

The resulting output (i.e., figures and tables) can be annotated and saved as a .jasp file. Output can then be shared with peers, with or without the real data in the .jasp file; if the real data are added, reviewers can easily reproduce the analyses, conduct alternative analyses, or insert comments.

Stereogram example

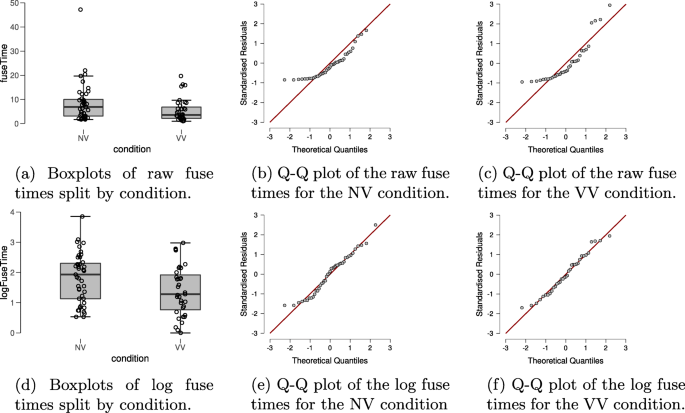
In order to check for violations of the assumptions of the t test, the top row of Fig. 2 shows boxplots and Q-Q plots of the dependent variable fuse time, split by condition. Visual inspection of the boxplots suggests that the variances of the fuse times may not be equal (observed standard deviations of the NV and VV groups are 8.085 and 4.802, respectively), suggesting the equal variance assumption may be unlikely to hold. There also appear to be a number of potential outliers in both groups. Moreover, the Q-Q plots show that the normality assumption of the t test is untenable here. Thus, in line with our analysis plan we will apply the log-transformation to the fuse times. The standard deviations of the log-transformed fuse times in the groups are roughly equal (observed standard deviations are 0.814 and 0.818 in the NV and the VV group, respectively); the Q-Q plots in the bottom row of Fig. 2 also look acceptable for both groups and there are no apparent outliers. However, it seems prudent to assess the robustness of the result by also conducting the Bayesian Mann–Whitney U test (van Doorn, Ly, Marsman, & Wagenmakers, 2020) on the fuse times.

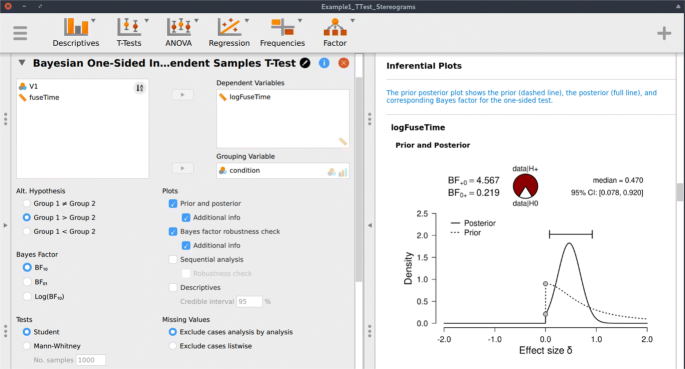
Following the assumption check, we proceed to execute the analyses in JASP. For hypothesis testing, we obtain a Bayes factor using the one-sided Bayesian two-sample t test. Figure 3 shows the JASP user interface for this procedure. For parameter estimation, we obtain a posterior distribution and credible interval, using the two-sided Bayesian two-sample t test. The relevant boxes for the various plots were ticked, and an annotated .jasp file was created with all of the relevant analyses: the one-sided Bayes factor hypothesis tests, the robustness check, the posterior distribution from the two-sided analysis, and the one-sided results of the Bayesian Mann–Whitney U test. The .jasp file can be found at https://osf.io/nw49j/. The next section outlines how these results are to be interpreted.

Stage 3: Interpreting the results

With the analysis outcome in hand, we are ready to draw conclusions. We first discuss the scenario of hypothesis testing, where the goal typically is to conclude whether an effect is present or absent. Then, we discuss the scenario of parameter estimation, where the goal is to estimate the size of the population effect, assuming it is present. When both hypothesis testing and estimation procedures have been planned and executed, there is no predetermined order for their interpretation. One may adhere to the adage “only estimate something when there is something to be estimated” (Wagenmakers et al., 2018) and first test whether an effect is present, and then estimate its size (assuming the test provided sufficiently strong evidence against the null), or one may first estimate the magnitude of an effect, and then quantify the degree to which this magnitude warrants a shift in plausibility away from or toward the null hypothesis (but see Box 3).

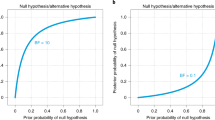
If the goal of the analysis is hypothesis testing, we recommend using the Bayes factor. As described in Box 1, the Bayes factor quantifies the relative predictive performance of two rival hypotheses (Wagenmakers et al., 2016; see Box 1). Importantly, the Bayes factor is a relative metric of the hypotheses’ predictive quality. For instance, if BF₁₀ = 5, this means that the data are 5 times more likely under \(<\mathscr>_\) than under \(<\mathscr>_\) . However, a Bayes factor in favor of \(<\mathscr>_\) does not mean that \(<\mathscr>_\) predicts the data well. As Figure 1 illustrates, \(<\mathscr>_\) provides a dreadful account of three out of four data sets, yet is still supported relative to \(<\mathscr>_\) .

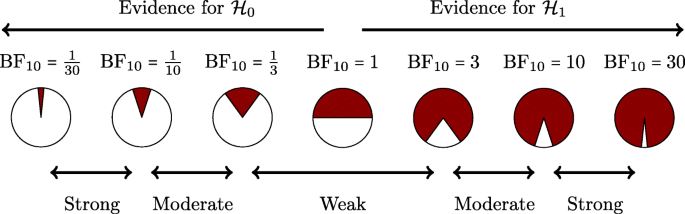
There can be no hard Bayes factor bound (other than zero and infinity) for accepting or rejecting a hypothesis wholesale, but there have been some attempts to classify the strength of evidence that different Bayes factors provide (e.g., Jeffreys, 1939; Kass & Raftery, 1995). One such classification scheme is shown in Figure 4. Several magnitudes of the Bayes factor are visualized as a probability wheel, where the proportion of red to white is determined by the degree of evidence in favor of \(<\mathscr>_\) and \(<\mathscr>_\) . Footnote 4 In line with Jeffreys, a Bayes factor between 1 and 3 is considered weak evidence, a Bayes factor between 3 and 10 is considered moderate evidence, and a Bayes factor greater than 10 is considered strong evidence. Note that these classifications should only be used as general rules of thumb to facilitate communication and interpretation of evidential strength. Indeed, one of the merits of the Bayes factor is that it offers an assessment of evidence on a continuous scale.

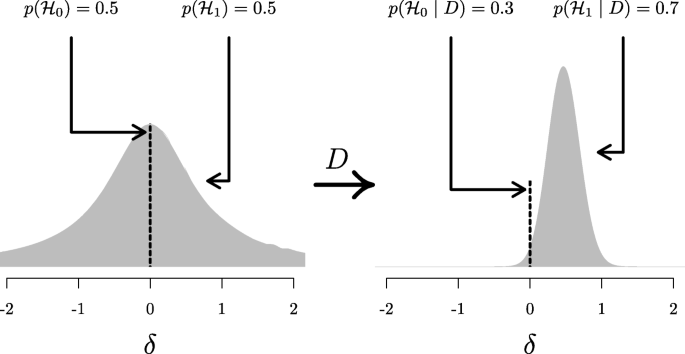
When the goal of the analysis is parameter estimation, the posterior distribution is key (see Box 2). The posterior distribution is often summarized by a location parameter (point estimate) and uncertainty measure (interval estimate). For point estimation, the posterior median (reported by JASP), mean, or mode can be reported, although these do not contain any information about the uncertainty of the estimate. In order to capture the uncertainty of the estimate, an x% credible interval can be reported. The credible interval [L,U] has a x% probability that the true parameter lies in the interval that ranges from L to U (an interpretation that is often wrongly attributed to frequentist confidence intervals, see Morey, Hoekstra, Rouder, Lee, & Wagenmakers, 2016). For example, if we obtain a 95% credible interval of [− 1,0.5] for effect size δ, we can be 95% certain that the true value of δ lies between − 1 and 0.5, assuming that the alternative hypothesis we specify is true. In case one does not want to make this assumption, one can present the unconditional posterior distribution instead. For more discussion on this point, see Box 3.

Box 3. Conditional vs. unconditional inference.

Common pitfalls in interpreting Bayesian results

Bayesian veterans sometimes argue that Bayesian concepts are intuitive and easier to grasp than frequentist concepts. However, in our experience there exist persistent misinterpretations of Bayesian results. Here we list five:

• The Bayes factor does not equal the posterior odds; in fact, the posterior odds are equal to the Bayes factor multiplied by the prior odds (see also Equation 1). These prior odds reflect the relative plausibility of the rival hypotheses before seeing the data (e.g., 50/50 when both hypotheses are equally plausible, or 80/20 when one hypothesis is deemed to be four times more plausible than the other). For instance, a proponent and a skeptic may differ greatly in their assessment of the prior plausibility of a hypothesis; their prior odds differ, and, consequently, so will their posterior odds. However, as the Bayes factor is the updating factor from prior odds to posterior odds, proponent and skeptic ought to change their beliefs to the same degree (assuming they agree on the model specification, including the parameter prior distributions).
• Prior model probabilities (i.e., prior odds) and parameter prior distributions play different conceptual roles. Footnote 5 The former concerns prior beliefs about the hypotheses, for instance that both \(<\mathscr>_\) and \(<\mathscr>_\) are equally plausible a priori. The latter concerns prior beliefs about the model parameters within a model, for instance that all values of Pearson’s ρ are equally likely a priori (i.e., a uniform prior distribution on the correlation parameter). Prior model probabilities and parameter prior distributions can be combined to one unconditional prior distribution as described in Box 3 and Fig. 5.
• The Bayes factor and credible interval have different purposes and can yield different conclusions. Specifically, the typical credible interval for an effect size is conditional on \(<\mathscr>_\) being true and quantifies the strength of an effect, assuming it is present (but see Box 3); in contrast, the Bayes factor quantifies evidence for the presence or absence of an effect. A common misconception is to conduct a “hypothesis test” by inspecting only credible intervals. Berger (2006, p. 383) remarks: “[. ] Bayesians cannot test precise hypotheses using confidence intervals. In classical statistics one frequently sees testing done by forming a confidence region for the parameter, and then rejecting a null value of the parameter if it does not lie in the confidence region. This is simply wrong if done in a Bayesian formulation (and if the null value of the parameter is believable as a hypothesis).”
• The strength of evidence in the data is easy to overstate: a Bayes factor of 3 provides some support for one hypothesis over another, but should not warrant the confident all-or-none acceptance of that hypothesis.
• The results of an analysis always depend on the questions that were asked. Footnote 6 For instance, choosing a one-sided analysis over a two-sided analysis will impact both the Bayes factor and the posterior distribution. For an illustration of this, see Fig. 6 for a comparison between one-sided and a two-sided results.

In order to avoid these and other pitfalls, we recommend that researchers who are doubtful about the correct interpretation of their Bayesian results solicit expert advice (for instance through the JASP forum at http://forum.cogsci.nl).

Stereogram example

For hypothesis testing, the results of the one-sided t test are presented in Fig. 6a. The resulting BF_{+ 0} is 4.567, indicating moderate evidence in favor of \(<\mathscr>_\) : the data are approximately 4.6 times more likely under \(<\mathscr>_\) than under \(<\mathscr>_\) . To assess the robustness of this result, we also planned a Mann–Whitney U test. The resulting BF_{+ 0} is 5.191, qualitatively similar to the Bayes factor from the parametric test. Additionally, we could have specified a multiverse analysis where data exclusion criteria (i.e., exclusion vs. no exclusion), the type of test (i.e., Mann–Whitney U vs. t test), and data transformations (i.e., log-transformed vs. raw fuse times) are varied. Typically in multiverse analyses these three decisions would be crossed, resulting in at least eight different analyses. However, in our case some of these analyses are implausible or redundant. First, because the Mann–Whitney U test is unaffected by the log transformation, the log-transformed and raw fuse times yield the same results. Second, due to the multiple assumption violations, the t test model for raw fuse times is misspecified and hence we do not trust the validity of its result. Third, we do not know which observations were excluded by (Frisby & Clatworthy, 1975). Consequently, only two of these eight analyses are relevant. Footnote 7 Furthermore, a more comprehensive multiverse analysis could also consider the Bayes factors from two-sided tests (i.e., BF₁₀ = 2.323) for the t test and BF₁₀ = 2.557 for the Mann–Whitney U test). However, these tests are not in line with the theory under consideration, as they answer a different theoretical question (see “Specifying the statistical model” in the Planning section).

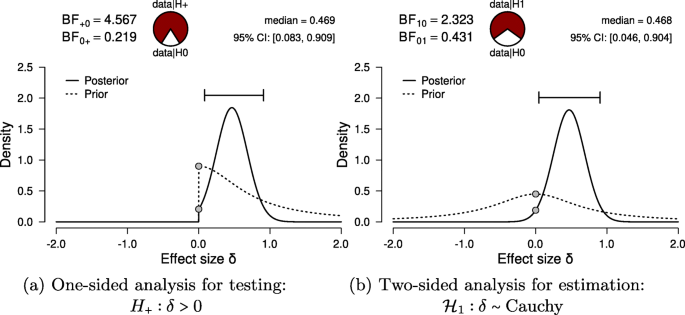
For parameter estimation, the results of the two-sided t test are presented in Fig. 6a. The 95% central credible interval for δ is relatively wide, ranging from 0.046 to 0.904: this means that, under the assumption that the effect exists and given the model we specified, we can be 95% certain that the true value of δ lies between 0.046 to 0.904. In conclusion, there is moderate evidence for the presence of an effect, and large uncertainty about its size.

Stage 4: Reporting the results

For increased transparency, and to allow a skeptical assessment of the statistical claims, we recommend to present an elaborate analysis report including relevant tables, figures, assumption checks, and background information. The extent to which this needs to be done in the manuscript itself depends on context. Ideally, an annotated .jasp file is created that presents the full results and analysis settings. The resulting file can then be uploaded to the Open Science Framework (OSF; https://osf.io), where it can be viewed by collaborators and peers, even without having JASP installed. Note that the .jasp file retains the settings that were used to create the reported output. Analyses not conducted in JASP should mimic such transparency, for instance through uploading an R-script. In this section, we list several desiderata for reporting, both for hypothesis testing and parameter estimation. What to include in the report depends on the goal of the analysis, regardless of whether the result is conclusive or not.

In all cases, we recommend to provide a complete description of the prior specification (i.e., the type of distribution and its parameter values) and, especially for informed priors, to provide a justification for the choices that were made. When reporting a specific analysis, we advise to refer to the relevant background literature for details. In JASP, the relevant references for specific tests can be copied from the drop-down menus in the results panel.

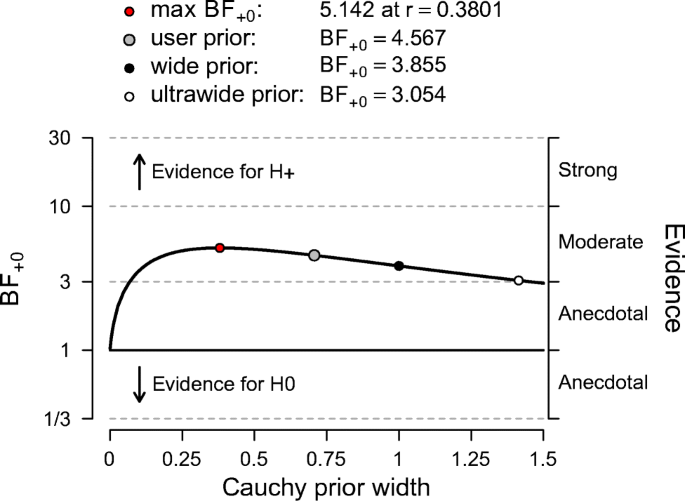
When the goal of the analysis is hypothesis testing, it is key to outline which hypotheses are compared by clearly stating each hypothesis and including the corresponding subscript in the Bayes factor notation. Furthermore, we recommend to include, if available, the Bayes factor robustness check discussed in the section on planning (see Fig. 7 for an example). This check provides an assessment of the robustness of the Bayes factor under different prior specifications: if the qualitative conclusions do not change across a range of different plausible prior distributions, this indicates that the analysis is relatively robust. If this plot is unavailable, the robustness of the Bayes factor can be checked manually by specifying several different prior distributions (see the mixed ANOVA analysis in the online appendix at https://osf.io/wae57/ for an example). When data come in sequentially, it may also be of interest to examine the sequential Bayes factor plot, which shows the evidential flow as a function of increasing sample size.

When the goal of the analysis is parameter estimation, it is important to present a plot of the posterior distribution, or report a summary, for instance through the median and a 95% credible interval. Ideally, the results of the analysis are reported both graphically and numerically. This means that, when possible, a plot is presented that includes the posterior distribution, prior distribution, Bayes factor, 95% credible interval, and posterior median. Footnote 8

Numeric results can be presented either in a table or in the main text. If relevant, we recommend to report the results from both estimation and hypothesis test. For some analyses, the results are based on a numerical algorithm, such as Markov chain Monte Carlo (MCMC), which yields an error percentage. If applicable and available, the error percentage ought to be reported too, to indicate the numeric robustness of the result. Lower values of the error percentage indicate greater numerical stability of the result. Footnote 9 In order to increase numerical stability, JASP includes an option to increase the number of samples for MCMC sampling when applicable.

Stereogram example

This is an example report of the stereograms t test example:

Here we summarize the results of the Bayesian analysis for the stereogram data. For this analysis we used the Bayesian t test framework proposed by (see also; Jeffreys, 1961; Rouder et al., 2009). We analyzed the data with JASP (JASP Team, 2019). An annotated .jasp file, including distribution plots, data, and input options, is available at https://osf.io/25ekj/. Due to model misspecification (i.e., non-normality, presence of outliers, and unequal variances), we applied a log-transformation to the fuse times. This remedied the misspecification. To assess the robustness of the results, we also applied a Mann–Whitney U test.

First, we discuss the results for hypothesis testing. The null hypothesis postulates that there is no difference in log fuse time between the groups and therefore \(<\mathscr>_: \delta = 0\) . The one-sided alternative hypothesis states that only positive values of δ are possible, and assigns more prior mass to values closer to 0 than extreme values. Specifically, δ was assigned a Cauchy prior distribution with \(r =/>\) , truncated to allow only positive effect size values. Figure 6a shows that the Bayes factor indicates evidence for \(<\mathscr>_\) ; specifically, BF_{+ 0} = 4.567, which means that the data are approximately 4.5 times more likely to occur under \(<\mathscr>_\) than under \(<\mathscr>_\) . This result indicates moderate evidence in favor of \(<\mathscr>_\) . The error percentage is < 0.001%, which indicates great stability of the numerical algorithm that was used to obtain the result. The Mann–Whitney U test yielded a qualitatively similar result, BF_{+ 0} is 5.191. In order to assess the robustness of the Bayes factor to our prior specification, Fig. 7 shows BF_{+ 0} as a function of the prior width r. Across a wide range of widths, the Bayes factor appears to be relatively stable, ranging from about 3 to 5.

Second, we discuss the results for parameter estimation. Of interest is the posterior distribution of the standardized effect size δ (i.e., the population version of Cohen’s d, the standardized difference in mean fuse times). For parameter estimation, δ was assigned a Cauchy prior distribution with \(r =/>\) . Figure 6b shows that the median of the resulting posterior distribution for δ equals 0.47 with a central 95% credible interval for δ that ranges from 0.046 to 0.904. If the effect is assumed to exist, there remains substantial uncertainty about its size, with values close to 0 having the same posterior density as values close to 1.

Limitations and challenges

The Bayesian toolkit for the empirical social scientist still has some limitations to overcome. First, for some frequentist analyses, the Bayesian counterpart has not yet been developed or implemented in JASP. Secondly, some analyses in JASP currently provide only a Bayes factor, and not a visual representation of the posterior distributions, for instance due to the multidimensional parameter space of the model. Thirdly, some analyses in JASP are only available with a relatively limited set of prior distributions. However, these are not principled limitations and the software is actively being developed to overcome these limitations. When dealing with more complex models that go beyond the staple analyses such as t tests, there exist a number of software packages that allow custom coding, such as JAGS (Plummer, 2003) or Stan (Carpenter et al., 2017). Another option for Bayesian inference is to code the analyses in a programming language such as R (R Core Team, 2018) or Python (van Rossum, 1995). This requires a certain degree of programming ability, but grants the user more flexibility. Popular packages for conducting Bayesian analyses in R are the BayesFactor package (Morey & Rouder, 2015) and the brms package (Bürkner, 2017), among others (see https://cran.r-project.org/web/views/Bayesian.html for a more exhaustive list). For Python, a popular package for Bayesian analyses is PyMC3 (Salvatier, Wiecki, & Fonnesbeck, 2016). The practical guidelines provided in this paper can largely be generalized to the application of these software programs.

Concluding comments

We have attempted to provide concise recommendations for planning, executing, interpreting, and reporting Bayesian analyses. These recommendations are summarized in Table 1. Our guidelines focused on the standard analyses that are currently featured in JASP. When going beyond these analyses, some of the discussed guidelines will be easier to implement than others. However, the general process of transparent, comprehensive, and careful statistical reporting extends to all Bayesian procedures and indeed to statistical analyses across the board.

Notes

The variables are participant number, the time (in seconds) each participant needed to see the hidden figure (i.e., fuse time), experimental condition (VV = with visual information, NV = without visual information), and the log-transformed fuse time.

A one-sided alternative hypothesis makes a more risky prediction than a two-sided hypothesis. Consequently, if the data are in line with the one-sided prediction, the one-sided alternative hypothesis is rewarded with a greater gain in plausibility compared to the two-sided alternative hypothesis; if the data oppose the one-sided prediction, the one-sided alternative hypothesis is penalized with a greater loss in plausibility compared to the two-sided alternative hypothesis.

The fat-tailed Cauchy distribution is a popular default choice because it fulfills particular desiderata, see (Jeffreys, 1961;Liang, German, Clyde, & Berger, 2008; Ly et al., 2016; Rouder, Speckman, Sun, Morey, & Iverson, 2009) for details.

Specifically, the proportion of red is the posterior probability of \(<\mathscr>_\) under a prior probability of 0.5; for a more detailed explanation and a cartoon see https://tinyurl.com/ydhfndxa

This is known as Jeffreys’s platitude: “The most beneficial result that I can hope for as a consequence of this work is that more attention will be paid to the precise statement of the alternatives involved in the questions asked. It is sometimes considered a paradox that the answer depends not only on the observations but on the question; it should be a platitude” (Jeffreys, 1939, p.vi).

The Bayesian Mann–Whitney U test results and the results for the raw fuse times are in the .jasp file at https://osf.io/nw49j/.

The posterior median is popular because it is robust to skewed distributions and invariant under smooth transformations of parameters, although other measures of central tendency, such as the mode or the mean, are also in common use.

We generally recommend error percentages below 20% as acceptable. A 20% change in the Bayes factor will result in one making the same qualitative conclusions. However, this threshold naturally increases with the magnitude of the Bayes factor. For instance, a Bayes factor of 10 with a 50% error percentage could be expected to fluctuate between 5 and 15 upon recomputation. This could be considered a large change. However, with a Bayes factor of 1000 a 50% reduction would still leave us with overwhelming evidence.

References

• Andrews, M., & Baguley, T. (2013). Prior approval: The growth of Bayesian methods in psychology. British Journal of Mathematical and Statistical Psychology, 66, 1–7. Google Scholar
• Anscombe, F. J. (1973). Graphs in statistical analysis. The American Statistician, 27, 17–21. Google Scholar
• Appelbaum, M., Cooper, H., Kline, R. B., Mayo-Wilson, E., Nezu, A. M., & Rao, S. M. (2018). Journal article reporting standards for quantitative research in psychology: The APA Publications and Communications Board task force report. American Psychologist, 73, 3–25. Google Scholar
• Berger, J. O. (2006). Bayes factors. In S. Kotz, N. Balakrishnan, C. Read, B. Vidakovic, & N. L. Johnson (Eds.) Encyclopedia of Statistical Sciences, vol. 1, 378-386, Hoboken, NJ, Wiley.
• Berger, J. O., & Wolpert, R. L. (1988) The likelihood principle, (2nd edn.) Hayward (CA): Institute of Mathematical Statistics. Google Scholar
• Bürkner, P.C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80, 1–28. Google Scholar
• Carpenter, B., Gelman, A., Hoffman, M., Lee, D., Goodrich, B., Betancourt, M., & et al. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76, 1–37. Google Scholar
• Clyde, M. A., Ghosh, J., & Littman, M. L. (2011). Bayesian adaptive sampling for variable selection and model averaging. Journal of Computational and Graphical Statistics, 20, 80–101. Google Scholar
• Depaoli, S., & Schoot, R. van de (2017). Improving transparency and replication in Bayesian statistics: The WAMBS-checklist. Psychological Methods, 22, 240–261. PubMedGoogle Scholar
• Dickey, J. M., & Lientz, B. P. (1970). The weighted likelihood ratio, sharp hypotheses about chances, the order of a Markov chain. The Annals of Mathematical Statistics, 41, 214–226. Google Scholar
• Dienes, Z. (2014). Using Bayes to get the most out of non-significant results. Frontiers in Psychology, 5, 781. PubMedPubMed CentralGoogle Scholar
• Draper, N. R., & Cox, D. R. (1969). On distributions and their transformation to normality. Journal of the Royal Statistical Society: Series B (Methodological), 31, 472–476. Google Scholar
• Etz, A. (2018). Introduction to the concept of likelihood and its applications. Advances in Methods and Practices in Psychological Science, 1, 60–69. Google Scholar
• Etz, A., Haaf, J. M., Rouder, J. N., & Vandekerckhove, J. (2018). Bayesian inference and testing any hypothesis you can specify. Advances in Methods and Practices in Psychological Science, 1(2), 281–295. Google Scholar
• Etz, A., & Wagenmakers, E. J. (2017). J. B. S. Haldane’s contribution to the Bayes factor hypothesis test. Statistical Science, 32, 313–329. Google Scholar
• Fisher, R. (1925). Statistical methods for research workers, (12). Edinburgh Oliver & Boyd.
• Frisby, J. P., & Clatworthy, J. L. (1975). Learning to see complex random-dot stereograms. Perception, 4, 173–178. Google Scholar
• Gronau, Q. F., Ly, A., & Wagenmakers, E. J. (2020). Informed Bayesian t tests. The American Statistician, 74, 137–143. Google Scholar
• Haaf, J., Ly, A., & Wagenmakers, E. (2019). Retire significance, but still test hypotheses. Nature, 567(7749), 461. PubMedGoogle Scholar
• Hinne, M., Gronau, Q. F., Bergh, D., & Wagenmakers, E. J. (2020). Van den A conceptual introduction to Bayesian model averaging. Advances in Methods and Practices in Psychological Science, 3, 200–215. Google Scholar
• Hoeting, J. A., Madigan, D., Raftery, A. E., & Volinsky, C. T. (1999). Bayesian model averaging: a tutorial. Statistical science, 382–401.
• JASP Team (2019). JASP (Version 0.9.2)[Computer software]. https://jasp-stats.org/.
• Jarosz, A. F., & Wiley, J. (2014). What are the odds? A practical guide to computing and reporting Bayes factors. Journal of Problem Solving, 7, 2–9. Google Scholar
• Jeffreys, H. (1939). Theory of probability, 1st. Oxford University Press.
• Jeffreys, H. (1961). Theory of probability. 3rd. Oxford University Press.
• Kass, R. E., & Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association, 90, 773–795. Google Scholar
• Keysers, C., Gazzola, V., & Wagenmakers, E. J. (2020). Using Bayes factor hypothesis testing in neuroscience to establish evidence of absence. Nature Neuroscience, 23, 788–799. PubMedPubMed CentralGoogle Scholar
• Lee, M. D., & Vanpaemel, W. (2018). Determining informative priors for cognitive models. Psychonomic Bulletin & Review, 25, 114–127. Google Scholar
• Liang, F., German, R. P., Clyde, A., & Berger, J. (2008). Mixtures of G priors for Bayesian variable selection. Journal of the American Statistical Association, 103, 410–424. Google Scholar
• Lo, S., & Andrews, S. (2015). To transform or not to transform: Using generalized linear mixed models to analyse reaction time data. Frontiers in Psychology, 6, 1171. PubMedPubMed CentralGoogle Scholar
• Ly, A., Verhagen, A. J., & Wagenmakers, E. J. (2016). Harold Jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology. Journal of Mathematical Psychology, 72, 19–32. Google Scholar
• Marsman, M., & Wagenmakers, E. J. (2017). Bayesian benefits with JASP. European Journal of Developmental Psychology, 14, 545–555. Google Scholar
• Matzke, D., Nieuwenhuis, S., van Rijn, H., Slagter, H. A., van der Molen, M. W., & Wagenmakers, E. J. (2015). The effect of horizontal eye movements on free recall: A preregistered adversarial collaboration. Journal of Experimental Psychology: General, 144, e1–e15. Google Scholar
• Morey, R. D., Hoekstra, R., Rouder, J. N., Lee, M. D., & Wagenmakers, E. J. (2016). The fallacy of placing confidence in confidence intervals. Psychonomic Bulletin & Review, 23, 103–123. Google Scholar
• Morey, R. D., & Rouder, J. N. (2015). BayesFactor 0.9.11-1. Comprehensive R Archive Network. http://cran.r-project.org/web/packages/BayesFactor/index.html.
• Plummer, M. (2003). JAGS: A Program for analysis of Bayesian graphical models using Gibbs sampling. In K. Hornik, F. Leisch, & A. Zeileis (Eds.) Proceedings of the 3rd international workshop on distributed statistical computing, Vienna, Austria.
• R Core Team (2018). R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria. https://www.R-project.org/.
• Rouder, J. N. (2014). Optional stopping: No problem for Bayesians. Psychonomic Bulletin & Review, 21, 301–308. Google Scholar
• Rouder, J. N., Haaf, J. M., & Vandekerckhove, J. (2018). Bayesian inference for psychology, part IV: Parameter estimation and Bayes factors. Psychonomic Bulletin & Review, 25(1), 102–113. Google Scholar
• Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225– 237. Google Scholar
• Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. (2016). Probabilistic programming in Python using pyMC. PeerJ Computer Science, 3(2), e55. Google Scholar
• Schönbrodt, F.D., & Wagenmakers, E. J. (2018). Bayes factor design analysis: Planning for compelling evidence. Psychonomic Bulletin & Review, 25, 128–142. Google Scholar
• Schramm, P., & Rouder, J. N. (2019). Are reaction time transformations really beneficial? PsyArXiv, March 5.
• Spiegelhalter, D. J., Myles, J. P., Jones, D. R., & Abrams, K. R. (2000). Bayesian methods in health technology assessment: a review. Health Technology Assessment, 4, 1–130. PubMedGoogle Scholar
• Steegen, S., Tuerlinckx, F., Gelman, A., & Vanpaemel, W. (2016). Increasing transparency through a multiverse analysis. Perspectives on Psychological Science, 11, 702–712. PubMedGoogle Scholar
• Stefan, A. M., Gronau, Q. F., Schönbrodt, F.D., & Wagenmakers, E. J. (2019). A tutorial on Bayes factor design analysis using an informed prior. Behavior Research Methods, 51, 1042–1058. PubMedPubMed CentralGoogle Scholar
• Sung, L., Hayden, J., Greenberg, M. L., Koren, G., Feldman, B. M., & Tomlinson, G. A. (2005). Seven items were identified for inclusion when reporting a Bayesian analysis of a clinical study. Journal of Clinical Epidemiology, 58, 261–268. PubMedGoogle Scholar
• The BaSiS group (2001). Bayesian standards in science: Standards for reporting of Bayesian analyses in the scientific literature. Internet. http://lib.stat.cmu.edu/bayesworkshop/2001/BaSis.html.
• Tijmstra, J. (2018). Why checking model assumptions using null hypothesis significance tests does not suffice: a plea for plausibility. Psychonomic Bulletin & Review, 25, 548–559. Google Scholar
• Vandekerckhove, J., Rouder, J. N., & Kruschke, J. K. (eds.) (2018). Beyond the new statistics: Bayesian inference for psychology [special issue]. Psychonomic Bulletin & Review, p 25.
• Wagenmakers, E. J., Beek, T., Rotteveel, M., Gierholz, A., Matzke, D., Steingroever, H., & et al. (2015). Turning the hands of time again: A purely confirmatory replication study and a Bayesian analysis. Frontiers in Psychology: Cognition, 6, 494. Google Scholar
• Wagenmakers, E. J., Lodewyckx, T., Kuriyal, H., & Grasman, R. (2010). Bayesian hypothesis testing for psychologists: A tutorial on the Savage–Dickey method. Cognitive Psychology, 60, 158–189. PubMedGoogle Scholar
• Wagenmakers, E. J., Love, J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., & et al. (2018). Bayesian inference for psychology. Part II: Example applications with JASP. Psychonomic Bulletin &, Review, 25, 58–76. Google Scholar
• Wagenmakers, E. J., Marsman, M., Jamil, T., Ly, A., Verhagen, J., Love, J., & et al. (2018). Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychonomic Bulletin &, Review, 25, 35–57. Google Scholar
• Wagenmakers, E. J., Morey, R. D., & Lee, M. D. (2016). Bayesian benefits for the pragmatic researcher. Current Directions in Psychological Science, 25, 169–176. Google Scholar
• Wetzels, R., Raaijmakers, J. G. W., Jakab, E., & Wagenmakers, E. J. (2009). How to quantify support for and against the null hypothesis: A flexible winBUGS implementation of a default Bayesian t test. Psychonomic Bulletin & Review, 16, 752– 760. Google Scholar
• Wicherts, J. M., Veldkamp, C. L. S., Augusteijn, H. E. M., Bakker, M., van Aert, R. C. M., & van Assen, M. A. L. M. (2016). Degrees of freedom in planning, running, analyzing, and reporting psychological studies: A checklist to avoid p-hacking. Frontiers in Psychology, 7, 1832. PubMedPubMed CentralGoogle Scholar
• Wrinch, D., & Jeffreys, H. (1921). On certain fundamental principles of scientific inquiry. Philosophical Magazine, 42, 369– 390. Google Scholar
• van Doorn, J., Ly, A., Marsman, M., & Wagenmakers, E. J. (2020). Bayesian rank-based hypothesis testing for the rank sum test, the signed rank test, and spearman’s rho. Journal of Applied Statistics, 1–23.
• van Rossum, G. (1995). Python tutorial (Tech. Rep. No. CS-R9526). Amsterdam: Centrum voor Wiskunde en Informatica (CWI).
• van den Bergh, D., Haaf, J. M., Ly, A., Rouder, J. N., & Wagenmakers, E. J. (2019). A cautionary note on estimating effect size. PsyArXiv. Retrieved from psyarxiv.com/h6pr8.

Acknowledgments

We thank Dr. Simons, two anonymous reviewers, and the editor for comments on an earlier draft. Correspondence concerning this article may be addressed to Johnny van Doorn, University of Amsterdam, Department of Psychological Methods, Valckeniersstraat 59, 1018 XA Amsterdam, the Netherlands. E-mail may be sent to johnnydoorn@gmail.com. This work was supported in part by a Vici grant from the Netherlands Organization of Scientific Research (NWO) awarded to EJW (016.Vici.170.083) and an advanced ERC grant awarded to EJW (743086 UNIFY). DM is supported by a Veni Grant (451-15-010) from the NWO. MM is supported by a Veni Grant (451-17-017) from the NWO. AE is supported by a National Science Foundation Graduate Research Fellowship (DGE1321846). Centrum Wiskunde & Informatica (CWI) is the national research institute for mathematics and computer science in the Netherlands.

Author information

Authors and Affiliations

1. University of Amsterdam, Amsterdam, Netherlands Johnny van Doorn, Don van den Bergh, Udo Böhm, Fabian Dablander, Tim Draws, Nathan J. Evans, Quentin F. Gronau, Julia M. Haaf, Max Hinne, Šimon Kucharský, Alexander Ly, Maarten Marsman, Dora Matzke, Akash R. Komarlu Narendra Gupta, Alexandra Sarafoglou, Angelika Stefan & Eric-Jan Wagenmakers
2. Nyenrode Business University, Breukelen, Netherlands Koen Derks
3. University of California, Irvine, California, USA Alexander Etz
4. Centrum Wiskunde & Informatica, Amsterdam, Netherlands Alexander Ly
5. Stanford University, Stanford, California, USA Jan G. Voelkel

1. Johnny van Doorn